Uma desenhista projetista deverá desenhar uma tampa de panela em forma circular. Para realizar esse desenho, ela dispõe, no momento, de apenas um compasso, cujo comprimento das hastes é de 10 cm, um transferidor e uma folha de papel com um plano cartesiano. Para esboçar o desenho dessa tampa, ela afastou as hastes do compasso de forma que o ângulo formado por elas fosse de 120º. A ponta seca está representada pelo ponto C, a ponta do grafite está representada pelo ponto B e a cabeça do compasso está representada pelo ponto A conforme a figura.
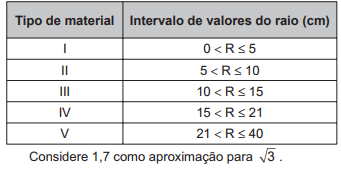
Após concluir o desenho, ela o encaminha para o setor de produção. Ao receber o desenho com a indicação do raio da tampa, verificará em qual intervalo este se encontra e decidirá o tipo de material a ser utilizado na sua fabricação, de acordo com os dados.
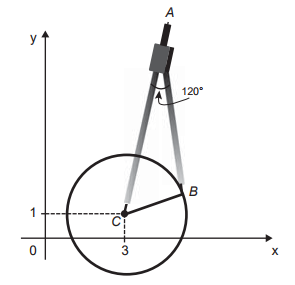
O tipo de material a ser utilizado pelo setor de produção será
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução Fácil e Rápida
Utilizando a lei dos cossenos no triângulo ABC:
BC2 = 102 + 102 – 2.10.10.cos(120º)
BC2 = 100 + 100 – 200.(-0,5)
BC2 = 300
BC = 10√3
BC = 17
Como esta medida está entre 15 e 21 cm, devemos usar o material IV.
Gabarito: (D)
Resolução Alternativa (Lei dos Senos)
O enunciado fornece um desenho feito com o auxílio de um compasso em que suas hastes medem 10 cm e sua abertura é de 120°. A questão consiste em calcular esse raio e verificar na tabela em que intervalo ele se encontra.
Observando o desenho, vemos que este consiste num triângulo isósceles cujos lados iguais (ie: pernas) são as hastes do compasso.
Dai vamos tentar descobrir os outros dois ângulos que podemos ver dentro desse triângulo. Sabemos que eles são congruentes pois trata-se de um triângulo isósceles. Chamando esse ângulo de α e aplicando a fórmula da soma dos ângulos internos:
2α + 120° = 180°
2α = 60°
α = 30°
Chamando de R o lado do triângulo o qual queremos saber seu valor (ie: o raio) e aplicando a lei do senos:
sen 30° / 10 = sen 120° / R
R sen 30° = 10 sen 120°
R.(1/2) = 10.(√3/2)
R/2 = 5√3
R = 10√3
Como o enunciado fornece que √3 = 1,7:
R = 10 . 1,7
R = 17 cm
Gabarito: (D)
