Em matemática, padrão é um arranjo de elementos (ex: figuras, letras, números …) que segue uma regra geral:
- Essa regra pode ser algo simples ou complicado, não há limite. O importante é ser bem definida.
- A quantidade de elementos também não tem limites, pode inclusive ser infinito. O importante é ter um mínimo de elementos para caracterizar a regra.
Diversos avanços na ciência ocorreram pois algum tipo de padrão foi identificado empiricamente. Alguns casos notórios são:
Crescimento Bacteriano
Sob condições ótimas, uma população de bactérias sofre um crescimento exponencial. Caso o tamanho dessa população seja medido em intervalos regulares de tempo, será obtido uma progressão geométrica (ex: 1, 2, 4, 8, 16 …).Lei de Ohm
A Lei de Ohm é uma generalização de diversos experimentos que demonstraram uma relação linear entre corrente e voltagem para diversos materiais. Caso a corrente seja medida em intervalos regulares de voltagem, será obtido uma progressão aritmética (ex: 1, 2, 3, 4, …).
Apenas várias décadas mais tarde é que encontrou-se modelos teóricos capazes de explicar essa lei.
Sequência e Progressão
Sequência é um tipo de padrão numérico. Ou seja, qualquer arranjo de números que siga uma regra geral bem definida, sem exceções, é uma sequência. A regra não precisa ser uma fórmula matemática, mas precisa ser bem definida. Exemplos:
Sequência dos Números Pares
{2, 4, 6, 8 …}Sequência dos Números Primos
ℙ = {2, 3, 5, 7, 11, …}
Progressão é outro tipo de padrão numérico. A diferença entre progressões e sequências é que progressões têm uma fórmula específica para calcular o n-enésimo termo. Portanto, nos exemplos acima:
- A sequência de números pares também é uma progressão pois podemos expressá-la pela fórmula an = 2n.
- No entanto, a sequência de números primos não tem uma fórmula e portanto não é uma progressão.
Progressão Aritmética
Na progressão aritmética cada termo é obtido adicionando ou
subtraindo um mesmo valor do termo anterior. Esse valor que é adicionado
ou subtraído é chamado de diferença comum ou
razão.
Podemos expressar uma progressão aritmética pela fórmula: an
= a1 + d.(n-1)
Exemplo:
Na sequência {1, 4, 7, 10, 13, …} cada termo é obtido ao adicionar 3 ao
anterior. Portanto, trata-se de uma progressão aritmética com diferença
comum igual a 3.
Progressão Geométrica
Numa progressão geométrica a regra consiste em multiplicar ou dividir
sempre por um mesmo valor para se obter o próximo termo. Esse valor é
chamado de razão.
Podemos expressar uma progressão geométrica pela fórmula: an
= a1 × r(n-1)
Exemplo:
Na sequência {2, 4, 8, 16, 32 …} cada termo é obtido multiplicando-se o
anterior por 2. Portanto, trata-se de uma progressão geométrica de razão
igual a 2.
Números Triangulares
A progressão triangular {1, 3, 6, 10, 15 …} pode ser representada visualmente através de triângulos equiláteros e, por isso, seus termos são chamados de números triangulares:
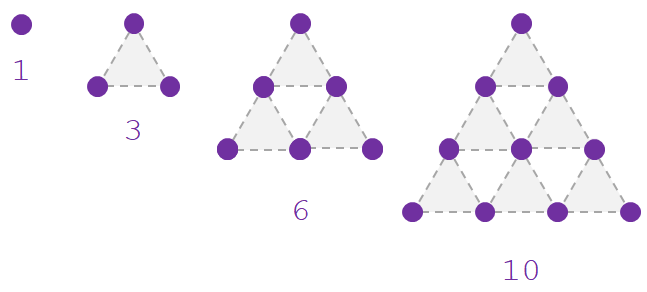
Podemos expressar a progressão triangular pela fórmula: an = (n2 + n)/2
Números Quadráticos
A progressão {1, 4, 9, 16, 25 …} pode ser representada visualmente através de quadrados. Por isso, é chamada de progressão quadrática e seus termos de números quadráticos.
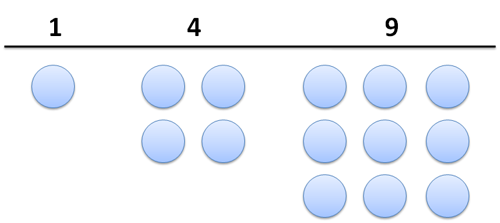
Podemos expressar uma progressão quadrática pela fórmula: an = n2
Números Cúbicos
A progressão {1, 8, 27, 64, 125 …} pode ser representada visualmente através de cubos. Por isso, é chamada de progressão cúbica e seus termos de números cúbicos.
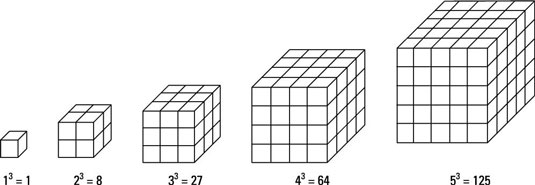
Podemos expressar uma progressão cúbica pela fórmula: an = n3
Números de Fibonacci
Numa progressão de Fibonacci, os termos são encontrados através da
adição dos dois termos anteriores. Ex: {0, 1, 1, 2, 3, 5, 8, 13 …}
A progressão de Fibonacci é nomeada por Leonardo Fibonacci, nascido em
1170 em Pisa, Itália. Fibonacci introduziu numerais hindu-arábicos para
os europeus com a publicação de seu livro “Liber Abaci” em 1202. Ele
também introduziu a progressão de Fibonacci, que já era conhecida pelos
matemáticos indianos. Essa progressão é importante, porque aparece em
diversos sistemas físicos distintos, incluindo: crescimento de
organismos (ex: plantas e conchas) e na formação de galáxias.
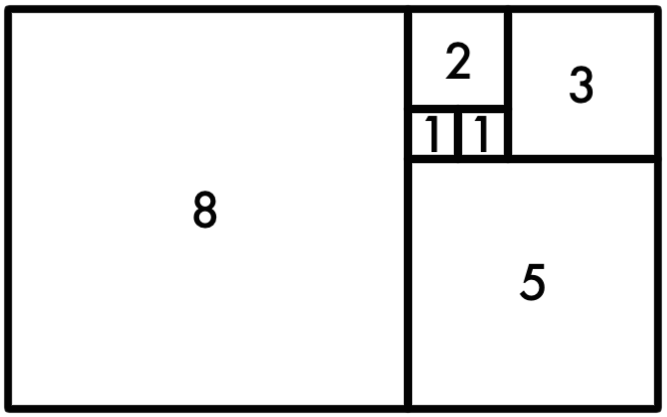
Assim como qualquer sequência definida por uma relação de recorrência linear, os números de Fibonacci também possuem uma fórmula fechada:
an = ( φn - (-φ)-n ) / √5
Onde φ é a razão áurea (1 + √5)/2
Essa fórmula ficou conhecida como fórmula de Binet.
Outras Sequências
As sequências acima são só algumas das mais famosas. No entanto, existem muitas outras:
| Nome | Primeiros Termos | Descrição |
|---|---|---|
| Tribonacci | {0, 1, 1, 2, 4, 7, 13, 24, 44, 81, …} | Semelhante aos números de Fibonacci, mas somando os 3 termos anteriores. |
| Garçom Preguiçoso | {1, 2, 4, 7, 11, 16, 22, 29, 37, 46, …} | O número máximo de pedaços formados ao fatiar uma panqueca com n cortes. |
| Vacas de Narayana | {1, 1, 1, 2, 3, 4, 6, 9, 13, 19, …} | O número de vacas por ano, se cada vaca tiver uma vaca por ano, começando no quarto ano. |
| Potências de Primos | {2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, …} | Potências inteiras de números primos. |
| Semi-primos | {4, 6, 9, 10, 14, 15, 21, 22, 25, 26, …} | Produto de dois primos, não necessariamente distintos. |
| Altamente Compostos | {1, 2, 4, 6, 12, 24, 36, 48, 60, 120, …} | Inteiro positivo com mais divisores que qualquer menor inteiro positivo. |
| Markov | {1, 2, 5, 13, 29, 34, 89, 169, 194, …} | Soluções positivas inteiras de x2 + y2 + z2 = 3xyz. |
| Números Compostos | {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, …} | Inteiros positivos que não são primos. |
| Números Aritméticos | {1, 3, 5, 6, 7, 11, 13, 14, 15, 17, 19, …} | Inteiros positivos que a média aritmética de seus divisores também é inteiro. |
| Sphenic | {30, 42, 66, 70, 78, 102, 105, 110, 114, …} | Produto de 3 primos distintos. |
| Paridade | {0, 1, 1, 0, 1, 0, 0, 1, 1, 0, …} | Complemento booleano da sequência até então. |
| Curva do Dragão | {1, 1, 0, 1, 1, 0, 0, 1, 1, 1, …} | Sobreposição da sequência alternada de 0s e 1s sobre ela própria. |
| Carol | {−1, 7, 47, 223, 959, 3967, 16127, 65023, …} | an = (2n - 1)2 - 2 |
| Números Educados | {3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, …} | Inteiro positivo que pode ser escrito como a soma de dois ou mais inteiros consecutivos. |
| Estrela | {1, 13, 37, 73, 121, 181, 253, 337, 433, …} | Sn = 6n(n − 1) + 1 |
| Stella octangula | {0, 1, 14, 51, 124, 245, 426, 679, 1016, …} | n(2n2 − 1) |
| Expoente Primo de Mersenne | {2, 3, 5, 7, 13, 17, 19, 31, 61, 89, …} | Primo p tal que 2p - 1 também é primo. |
| Primos de Mersenne | {3, 7, 31, 127, 8191, 131071, 524287, …} | 2p - 1 é primo. |
| Primos de Sophie Germain | {2, 3, 5, 11, 23, 29, 41, 53, 83, 89, …} | 2p+1 é primo. |
| Palíndromos | {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, …} | O número permanece o mesmo invertendo a ordem de seus dígitos. |
Nas Provas de Raciocínio-Lógico
Nas provas de raciocínio-lógico (concursos, vestibular, MBA, QI, …) é comum haver algumas variações dos tipos de sequências descritos acima. Essas variações não costumam ser complicadas, mas pra quem nunca viu pode ficar difícil de detectar no curto tempo da prova. Portanto, é importante estudá-las com antecedência. Tais variações mais comuns são:
Operações Alternadas
O termo é calculado alternando-se algumas das operações elementares. O mais comum é alternar entre adição e multiplicação. Exemplo:3 5 10 12 24 26 ... (+2) (×2) (+2) (×2) (+2)Operações Monótonas
O termo é calculado através de uma adição em que o adendo cresce monotonicamente. Exemplo:3 5 8 12 17 23 ... (+2) (+3) (+4) (+5) (+6)Sequências Entrelaçadas
Quando duas sequências distintas são combinadas numa só. Exemplo:Números Quadráticos: 1 4 9 16 25 … Números Primos: 2 3 5 7 11 … Sequência Entrelaçada: {1, 2, 4, 3, 9, 5, 16, 7, 25, 11, ...}Sequências Cíclicas
A sequência percorre um intervalo definido e, ao chegar no final, volta ao início do intervalo.
Nesse caso, o mais comum é usar minutos e segundos. Exemplo:{0, 25, 50, 15, 40, 5, 30, 55, 20, …}
Note que no exemplo acima é como se o ponteiro dos segundos estivesse saltando de 25 em 25 segundos.
Dígitos
A regra da sequência atua diretamente sobre os dígitos do número. Exemplo:{109, 218, 327, 436, 545, 654, 763, …}
Note que nos dois primeiros dígitos adiciona-se +1 pra cada termo. Enquanto que no último dígito é subtraído -1 pra cada termo.
Soluções Criativas
Qualquer regra bem definida pode ser usada pra gerar sequências, inclusive algumas bem criativas. Exemplos:- ordem alfabética: {5, 10, 2, 12, 9, 8, 11, 4, 6, 7, 3, 13, 1, 0}
- dígitos do π: {3, 1, 4, 1, 5, 9, 2, 6 …}
- veja e diga: {1, 11, 21, 1211, 1231, 131221, …}
“tem um um”, “tem dois um”, “tem um dois e um um”, “tem um dois e três um”, …
