CNU 2024: Matemática | (prova)
Bloco 8 - Nível Intermediário
Questão 22
Em uma fábrica, há dois tanques, um no formato de um cilindro circular reto, com raio de base medindo R e altura medindo 2y, e outro no formato de um cone circular reto, com raio de base medindo 2R e altura medindo y, como indicado na Figura.
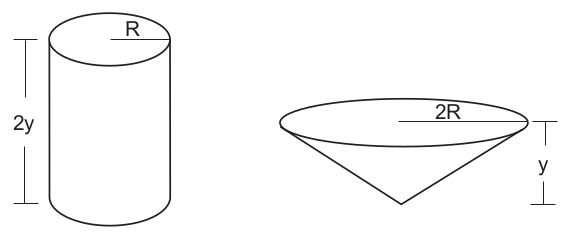
Considere que esses dois tanques estejam inicialmente vazios e despreze a espessura de suas superfícies. Sabe-se que uma torneira, de vazão constante, levou 2 h 24 min para encher completamente o tanque cilíndrico.
O tempo necessário e suficiente para que essa mesma torneira, com a mesma vazão, encha completamente o tanque cônico é de
(A) 1 h 24 min
(B) 1 h 36 min
(C) 1 h 54 min
(D) 2 h 24 min
(E) 3 h 36 min
Resolução
O volume do tanque cilíndrico é:
V1 = πr²h
V1 = 2πR²y
O volume do tanque cônico é:
V2 = πr²h/3
V2 = π(2R)²y/3
V2 = 4πR²y/3
Podemos usar a seguinte fórmula pra vazão da torneira:
q = V/Δt
Como em ambos os casos a vazão é a mesma:
q1 = q2
V1/Δt1 = V2/Δt2
Δt2 = Δt1 . V2/V1
Δt2 = Δt1 . (2/3)
Sabemos que Δt1 = 2h:24min. Transformando para minutos temos Δt1 = 144min. Daí:
Δt2 = 144 . (2/3)
Δt2 = 96 min
Transformando Δt2 pro formato horas:minutos temos:
Δt2 = 1h:36min
Gabarito: (B)
